GTU Probability and Statistics (P&S) Summer 2022 Paper Solutions

Q.1

(a) Define and give the example of: (i) Random variable, (ii) Independent Events. (03 marks)

(i) Random Variable: A random variable assigns numerical values to outcomes of a random process. For example, rolling a fair six-sided die can be represented by a random variable, say X, with values {1, 2, 3, 4, 5, 6}.

(ii) Independent Events: Two events are independent if the occurrence of one doesn't affect the other. In tossing two coins, let A be the first coin landing heads and B the second coin landing heads. A and B are independent since the outcome of the first toss doesn't influence the second. The probability of both events happening is calculated by multiplying their individual probabilities: P(A and B) = P(A) * P(B).

(b) Two fair six-sided dice are tossed independently. Let M be the maximum of the two tosses. What is the probability mass function (pmf) of M? (04 marks)

S = {

(1,1) (1,2) (1,3) (1,4) (1,5) (1,6)

(2,1) (2,2) (2,3) (2,4) (2,5) (2,6)

(3,1) (3,2) (3,3) (3,4) (3,5) (3,6)

(4,1) (4,2) (4,3) (4,4) (4,5) (4,6)

(5,1) (5,2) (5,3) (5,4) (5,5) (5,6)

(6,1) (6,2) (6,3) (6,4) (6,5) (6,6)

}

M	1	2	3	4	5	6
P(M)	1/36	3/36	5/36	7/36	9/36	11/36	⇒ Total : 1

(c) Seventy percent of the light aircraft that disappear while in flight in a certain country are subsequently discovered. Of the aircraft that are discovered, 60% have an emergency locator, whereas 90% of the aircraft not discovered do not have such a locator. Suppose a light aircraft has disappeared.

(i) If it has an emergency locator, what is the probability that it will not be discovered? (ii) If it does not have an emergency locator, what is the probability that it will be discovered? (7)

P(D)=0.70 , P(E/D)= 0.60 , P(E’/D’)=0.90

P(D’)=0.30, P(E’/D)= 0.40, P(E /D’)=0.10

i.) $P(\overline{D}/E) = \frac{ P(\overline{D}).P(E/\overline{D})}{P(\overline{D}).P(E/\overline{D}) + P(D)P(E/D)} = 0.0667$

ii.) $P(D/\overline{E}) = \frac{ P(D).P(\overline{E}/D)}{P(D)P(\overline{E}/D) + P(\overline{D}) P(\overline{E}/\overline{D})} = 0.5091$

Q.2

(a) State the probability function of Exponential and Gamma distribution. (3 marks)

Exponential Distribution:

The probability density function (PDF) of the Exponential distribution is given by:

$f(x;λ)=λe^{−λx}$

Where:

• x is the random variable.
• λ (lambda) is the rate parameter, which is the inverse of the mean. It determines the shape of the distribution.

Gamma Distribution:

The probability density function (PDF) of the Gamma distribution is given by:

$f(x;k,θ)= \frac{1}{Γ(k)⋅θ^k}​⋅x^{k−1}e^{−\frac{x}{θ}}​$

Where:

• x is the random variable.
• k is the shape parameter.
• θ is the scale parameter.
• Γ(k) is the gamma function, which is a generalization of the factorial function for non-integer values.

(b) A dice is thrown 264 times with the following results. Show that the dice is biased. [Use $𝜒 ^20.05$ for 5 degree of freedom]. (4)

No. appeared on dice	1	2	3	4	5	6
Frequency	40	32	28	58	54	52

Ans:

Fo	Fe	(Fo-Fe)^2/Fe
40	44	0.3636
32	44	3.2727
28	44	5.8182
58	44	4.4545
54	44	2.2727
52	44	1.4545
		17.6362

1. H0 : Dice is Unbiased
2. H1 : Dice is biased
3. α : 0.05
4. $x^2 = \frac{∑(Fo-Fe)^2}{Fe} = 17.6362$$Fe = \frac{264}{6} = 44$

5. V = N -1 = 6-1 = 5

   $X^2_{0.05}(V=5) = 11.07$
6. $x^2>x^2_{0.05}$ **Rejected**

(c) Fit a straight line to the following data. Also, estimate the value of y at x=72. (7)

x	65	66	67	67	68	69	71	73
y	67	68	64	68	72	70	69	70

y = a+bx

Ey = na + bEx

Exy = $aEx+bEx^2$

a=39.54 n = 8

b = 0.4242

x	y	x^2	xy
546	548	37314	37422

estimate x=72,

y=39.5455 + 0.4242 (72)

y = 70.0910

OR

(c) Fit the second degree parabola using the least square method to the following data: Also, estimate y at x=6. (7)

x	1	2	3	4	5
y	5	12	26	60	97

$y =a+bx+cx^2$$Ey =na+ bEx+cEx^2$$Exy = aEx+ bEx^2 + cEx^3$$Ex^2y = aEx^2+ bEx^3+cEx^4$

	x	y	x^2	x^3	x^4	xy	x^2 y
E =	15	20	55	225	979	832	3672

a = 10.4 , b= -11.0857, c=5.71

y = (10.4) - (11.0857) (x) + (5.71) $x^2$

put x=6,

y=149.6

Q.3

(a) State the properties of the Normal Distribution (03 marks)

Properties of normal distribution:

1. It is symmetric
2. Its mean/median/mode are equal

(b) If a random variable has a Poisson distribution such that P(X=1)=P(X=2), find

(i) the mean of the distribution, (ii) P(X=5), (iii) P(X>1), and (iv) P(1<X<4) (04 marks)

$P(X=x) = \frac{e^{-λ}λ^x}{x1}$

P(X=1) = P(X=2)

$\frac{e^{-λ}λ^x}{1!} = \frac{e^{-λ}λ^x}{2!}$

λ = 2

1. Mean = λ = 2
2. P (X=5) = $\frac{e^{-λ}λ^5}{5!} = 0.0361$

3. P(X>1) = 1 - P(x≤1)

   1 - [ P(x=0) + P(x=1) ]

   1 - [ 0.1353 + 0.2707 ]

   0.5940

4. P(1<x<4) = P(x=2) + P(x=3)

   0.4511

(c) Define Binomial Distribution. A particular telephone number is used to receive both voice calls and fax messages. Suppose that 25% of the incoming calls involve fax messages, and consider a sample of 10 incoming calls. What is the probability that

(i)At most 3 (ii) Exactly 3 (iii) At least 3 (iv) More than 3, of the calls involve a fax message?

Binomial Distribution : The binomial distribution is a discrete probability distribution that describes the number of successes in a fixed number of independent Bernoulli trials, where each trial has only two possible outcomes: success or failure. The outcomes are often denoted as "success" and "failure," but they can represent any dichotomous events, such as heads or tails in a coin flip, true or false in a survey, etc.

P(X=x) = $nCx. P^x. q^{n-x}$

P=0.25

n=10

q = 1-p = 0.75

1. P(x≤3) = P(x=0) + p(x=1) + p(x=2) + p(x=3)

   0.0563 + 0.187 + 0.281 + 0.2503

   0.7759

2. P(x=3) = 0.2503

3. P(x≥3) = 1-P(x<3)

   1 - ( P(x=0) + P(x=1) + P(x=2) )

   0.4744

4. P(x>3) = 1 - p(x≤3) = 0.2241

OR

Q.3

(a) The mean and variance of a binomial distribution are 4 and 2. Find 𝑃(𝑋≥2). (03 marks)

Mean = np = 4

Variance = npq = 2

$\frac{np}{npq} = \frac{4}{2}$$p = 1-q = \frac{1}{2}$$\frac{1}{q}= 2 , q = \frac{1}{2}$$n(\frac{1}{2})=4, n=8$

P(x≥2) = 1-P(x<2) = 1[P(x=0)+P(x=1)] = 1 - [0.0039+0.0313] = 0.9649

(b) A car hire firm has two cars, which it hires out day by day. The number of demands for a car on each day is distributed as a Poisson distribution with mean of 1.5. Calculate the proportion of days on which

(i) neither car is used, (ii) some demand is refused, (iii) only one car is used. (04 marks)

λ=1.5 P(X=x) = $\frac{e^{-λ}λ^x}{x!}$

1. P(x=0) = $\frac{e^{-λ}λ^x}{0!}=0.2231$

2. P(x>2) = 1 - P(x≤2) = 1 - [P(x=0) + P(x=1) + P(x=2)]

   = 0.1912

3. P(x=1) = $\frac{e^{-λ}λ^1}{1!} = 0.3347$

(c) Define Standard normal variate. The lifetime of a certain kind of batteries has a mean life of 400 hours and the standard deviation as 45 hours. Assuming the distribution of lifetime to be normal. Find The percentage of batteries with lifetime (i) at least 490 hours, (ii) between 385 and 490 hours. Also, find the minimum life of the best 5% of batteries.

[Use: P(0< z < 2) = 0.4772, P(0 < z < 0.33) = 0.1293 and P(0< z < 1.65) = 0.45] (7 marks)

$z= \frac{X- μ}{σ}$ (Define)

μ=400, σ=45

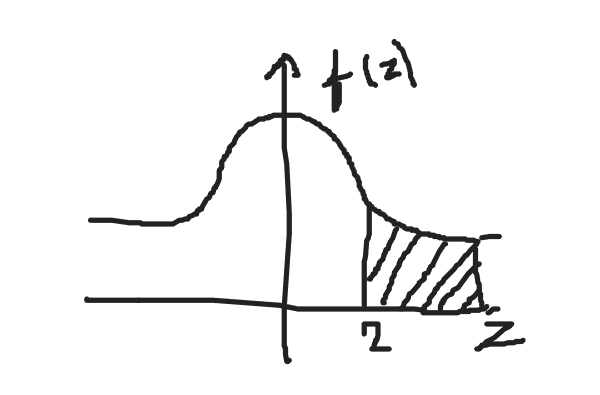
1. P(x≥490), $z=\frac{490-400}{45}=2$

   P(z≥2) = P(0<z<∞) - P(0<z<2) = 0.5-04772 = 0.0228 = 2.28%

2. P(385<x<490) $z_1= \frac{x_1 - μ}{σ} = -0.33$$z_2=2$

   P(-0.33<z<2)

   = P(-0.33<z<0) + P(0<z<2)

   = P(0<z<0.33) + P(0<z<2)

   = 0.1293 + 0.4772

   = 0.6065

   = 60.65%

3. let min life of best 5% battery is x1

   P(x≥x1) = 0.05 (5%)

   P(z≥z2) = 0.05

   

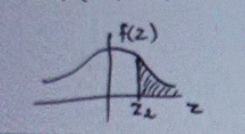
   P(0<z<2) = P(0<z<∞) - P(x2<z<∞)

   = 0.5-0.05

   = 0.45

   P(0<z<1.65) = 0.45 (given)

   z2 = 1.65

   z2 = $\frac{x_1-μ}{σ}$

   $1.65 = \frac{x_1-400}{45}$

   x1 = 474.25 hours

Q.4

(a) Explain the term related to testing of hypothesis:

(i) Type I Error, (ii) Type II Error, (iii) Level of Significance. (03 marks)

(i) Type I Error: A Type I error occurs in hypothesis testing when the null hypothesis (H0) is incorrectly rejected when it is actually true. In other words, it is the error of concluding that there is a significant effect or difference when, in reality, there is none. The probability of committing a Type I error is denoted by the symbol α (alpha) and is referred to as the significance level.

(ii) Type II Error: A Type II error occurs when the null hypothesis is not rejected when it is false. In this case, the test fails to detect a significant effect or difference that really exists. The probability of committing a Type II error is denoted by the symbol β (beta).

(iii) Level of Significance: The level of significance, often denoted by α (alpha), is the predetermined probability of committing a Type I error in hypothesis testing. It represents the maximum acceptable probability of rejecting a true null hypothesis. Commonly used levels of significance include 0.05 (5%) and 0.01 (1%). Researchers choose the level of significance based on the desired balance between the risk of making a Type I error and the desire for a more stringent test.

(b) A coin was tossed 960 times and returned heads 183 times. Test the hypothesis that the coin is unbiased. Use 5% level of significance. [use $𝑍_{0.05}=1.96$ ]. (04 marks)

n = 960 (large sample)

p=0.5 , q=0.5

x = 183, μ = np = 480, $σ = \sqrt{npq}{1} = 15.49$

1. H0 = coin is unbiased
2. H1 = coin is biased
3. α = 0.05
4. $z=\frac{x-μ}{σ}=-19.1713$

   |z| = 19.1713

5. $z_{0.05} =1.96$

6. |z| >$|z_{0.05}|$

   Rejected

(c) Two types of batteries are tested for their length of life and the following data are obtained:

	No. of samples	mean life in hours	Variance
Type A	9	600	121
Type B	8	640	144

Is there a significant difference in the two means? [Use $𝑡_{0.05,15} = 2.132$]

diff. or 2 mean

n1 = 9

n2 = 8

$\bar{x_1} = 600$$\bar{x_2} = 640$${s_1}^2 = 121$${s_2}^2 = 144$$s = \sqrt{\frac{n_1{s_1}^2 + n_2{s_2}^2}{n_1+n_2-2}}$

= 12.2229

1. $H_0 : μ_1 = μ_2$
2. $H_1: μ_1 \ne μ_2$
3. α = 0.05
4. $t = \frac{\bar{x_1}-\bar{x_2}}{\sqrt{\frac{1}{n_1} + \frac{1}{n_2}}}$

   = -6.7348

   |t| = 6.7348

5. V = $n_1+n_2-2= 15$

   $t_{0.05} = 2.132$

6. |t| > |$t_{0.05}$|

   Rejected

OR

Q.4

(a) Ten objects are chosen at random from a large population and their weights are found to be in grams:61,63,64,65,68,69,69,70,71,71. Discuss the suggestion that the mean is 65 g. [Use 𝑡0.05 = 2.262 𝑎𝑡 𝑣 = 9]. (03 marks)

n=10, μ=65

1. H0 : μ=65g
2. H1 : μ ≠ 65g
3. α = 0.05
4. $t=\frac{\bar{x}-μ}{\sqrt{n-1}}$

   = 1.8586

5. $t_{0.05}(V=9) = 2.2632$

   V=n-1

   = 10-1

   = 9

6. |t| < $|t_{0.05}|$

   Accepted

(b) The means of simple samples of sizes 1000 and 2000 are 67.5 cm and 68 cm respectively. Can the samples be regarded as drawn from the same population of standard deviation 2 cm. [use 𝑍0.05 = 1.96] (04 marks)

large sample diff of mean

$n_1= 1000, n_2=2000$$\bar{x_1}=67.5, \bar{x_2} = 68$$σ_1=2,σ_2=2$

1. $H_0: μ_1 = μ_2$
2. $H_1:μ_1 \ne μ_2$
3. α = 0.05
4. $z=\frac{\bar{x_1}-\bar{x_2}}{\sqrt{ \frac{{σ_1}^2}{n_1} + \frac{{σ_2}^2}{n_2}}} = -6.4500$

   |z| = 6.4550

5. $z_{0.05} = 1.96$
6. |z| > $|z_{0.05}|$ = Rejected

(c) Two random samples are drawn from two populations and the following results were obtained:

Sample I	21	24	25	26	27
Sample II	22	27	28	30	31	36

Find the variances of the two samples and test whether the two populations have the same variances.[Use $𝐹_{0.05}(5,4) = 6.26.$]

small sample testt

$\bar{x_1} = 24.6, \bar{x_2}= 29$$n_1=5, n_2=6$

12.96	49
0.36	4
0.16	1
1.96	1
5.76	4
	49
21.2	108

${S_1}^2=\frac{Σ(x_1-\bar{x1})^2}{n_1}=\frac{21.2}{5}=4.24$${S_2}^2=\frac{Σ(x_2-\bar{x2})^2}{n_2}=\frac{108}{6}=18$${S_1}^2=\frac{(n_1s_1)^2}{n_1-1}=\frac{5 X 4.24}{4}=5.3$${S_2}^2=\frac{(n_2s_2)^2}{n_2-1}=\frac{6 X 18}{5}=21.6$

1. $H_0: {σ_1}^2 = {σ_2}^2$
2. $H_1: {σ_1}^2 \ne {σ_2}^2$
3. α = 0.05
4. F = $\frac{{S_2}^2}{{S_1}^2} = \frac{21.6}{5.3} = 4.0755$
5. $n_1-1=4, n_2-1=5$$F_{0.05}(4,5) = 6.26$
6. $F < F_{0.05}$

Accepted

Q.5

(a) The probability distribution of a random variable X is given below. Find (i) E(X), (ii) V(X)

X	-2	-1	0	1	2
P(x=X)	0.2	0.1	0.3	0.3	0.1

$E(X) = Σx_iP(x_i)=(-2)(0.2)+....+(2)(0.1)=0$$V(x)=E(x^2)-[E(x)]^2$$Σ{x_1}^2P(x_i)-(0)^2$$[(-2)^2(0.2)+....+(2)^2(0.1)]-0=1.6$

(b) The following are the lines of regression 9𝑦 = 𝑥 + 288 𝑎𝑛𝑑 4𝑦 = 𝑥 + 38. Estimate y when x = 99 and x when y = 30. Also, find the means of x and y

9y = x+288 ——(1)

4y=x+38 ——(2)

$y=\frac{1}{9}x+\frac{288}{9}$

x=4y-38

$byx=\frac{1}{9}$

byx=4

x=99 put,

y=30, put

y=43

x=82

solve eqn (1) & (2)

$\bar{y}=50$$\bar{x}=162$

(c) Ten competitors in a test are ranked by three judges in the following order:

Rank by first Judge	6	10	2	9	8	1	5	3	4	7
Rank by second Judge	5	4	10	1	9	3	8	7	2	6
Rank by third judge	4	8	2	10	7	5	9	1	3	6

Use the method of rank correlation to gauge which pairs of judges has nearest common approach.

x	y	z	d1 ^ 2	d2 ^ 2	d3 ^ 2
			1	1	4
			36	16	4
			64	64	0
			64	81	1
			1	4	1
			4	4	16
			9	1	16
			16	36	4
			4	1	1
			1	0	1
			Σ=200	208	48

$r_1=1-\frac{σΣ{d_1}^2}{n(n^2-1)} = -0.2121$$r_2=1-\frac{σΣ{d_2}^2}{n(n^2-1)} = 0.2606$$r_3=1-\frac{σΣ{d_3}^2}{n(n^2-1)} = 0.7091$

r3 = MAX = x&z

judge 1 & 3

nearest common approach.

OR

Q.5

(a) For a group of 10 items, $Σ𝑥 = 452$, $Σ𝑥^2 = 24270$, 𝑎𝑛𝑑 $𝑚𝑜𝑑𝑒 = 43.7$. Find Karl Pearson’s coefficient of Skewness.

$S_k= \frac{mean-mode}{SD} = 0.0766$$SD = \sqrt{\frac{Σx^2}{n} - (\frac{Σx}{n})^2} = 19.5949$

n = 10

Σx = 452

$Σx^2=24270$

Mean = $\frac{Σx}{n} = \frac{452}{10} = 45.2$

(b) Find the correlation coefficient for the following data:

X	-3	-2	-1	0	1	2	3
Y	9	4	1	0.5	1	4	9

$r = \frac{Σ(x-\bar{x})(y-\bar{y})}{\sqrt{Σ(x-\bar{x})^2}\sqrt{Σ(y-\bar{y})^2}}$

= 0

$\bar{x}=\frac{Σx}{n}=0 ↙ \frac{0}{7}$$\bar{y}=\frac{Σy}{n}=4.0714$

(c) Calculate the regression coefficients and find the two lines of regression for the following data:

X	57	58	59	59	60	61	62	64
Y	67	68	65	68	72	72	69	71

Find the value of y when x=65.

$byx = \frac{Σ(x-\bar{x})(y-\bar{y})}{Σ(x-\bar{x})^2}$$bxy = \frac{Σ(x-\bar{x})(y-\bar{y})}{Σ(y-\bar{y})^2}=24/44=0.5455$$\bar{x}=\frac{Σx}{n} = \frac{480}{8} = 60$$\bar{y}=\frac{Σy}{n} = \frac{552}{8} = 69$

Reg y on x,

$y-\bar{y}=byx(x-\bar{x})$

y = 0.6667x + 29

put, x=65

y=72.33

Reg x on y,

$x-\bar{x} = bxy(y-\bar{y})$

x=0.5455y + 22.36