GTU Discrete Mathematics Summer 2021 Paper Solution

Download Question Paper : click here

Q.1

(a) Among 100 people at least how many of them were born in the same month?

⇒ Let n = 100 (Pigeon)

⇒ let k = 12 (Pigeon Holes)

⇒ So the minimum Number of people who we born in same month = ⌈ n/k ⌉ = ⌈ 100 / 12 ⌉ = 9

⇒ At least 9 people are born in same month.

(b) Prove that:  (A U B)' = A' ∩ B'.

Let R = (A U B)' and S = A' ∩ B'. Suppose we choose an element y that belongs to R. This is denoted as y ∈ R.

⇒ y ∈ (A U B)'

⇒ y ∉ (A U B)

⇒ y ∉ A and y ∉ B

⇒ y ∈ A' and y ∈ B'

⇒ y ∈ A' ∩ B'

⇒ y ∈ S

Thus, we conclude that R ⊂ S (R is a subset of S) ...(1)

Now suppose we have an arbitrary element z that belongs to set S. Then z ∈ S

⇒ z ∈ A' ∩ B'

⇒ z ∈ A' and z ∈ B'

⇒ z ∉ A and z ∉ B

⇒ z ∉ (A U B)

⇒ z ∈ (A U B)'

⇒ z ∈ R

Hence, S ⊂ R ...(2)

From (1) and (2) we infer that S = R or (A ∪ B)’ = A’ ∩ B’. Thus, this theorem is proved.

(c).Define the following:

1) Composition of functions : The composition of a function is an operation where two functions say f and g generate a new function say h in such a way that h(x) = g(f(x)).

2) Monoid : A monoid is a set that is closed under an associative binary operation and has an identity element such that for all.

OR

An Algebraic Structure(A,*) is called Monoid if it satisfy following properties:

1. • is closed on A.2. is Associative of A3. There exits an identity element with respect to .

2. is Associative of A*

3. There exits an identity element with respect to .*

3) Existential Quantifier : Let for the predicate p(x), for all x p(x) is false, but there exits at least one value of  x for which p(x) is true, Then we can say that x is bounded by existential quantification.

4) Partially Ordered Set : Consider a relation R on a set S satisfying the following properties:

• R is reflexive, i.e., xRx for every x ∈ S.
• R is antisymmetric, i.e., if xRy and yRx, then x = y.
• R is transitive, i.e., xRy and yRz, then xRz.

Then R is called a partial order relation, and the set S together with partial order is called a partially order set or POSET and is denoted by (S, ≤).

5) Boolean Algebra : Boolean algebra is the branch of algebra in which the values of the variables are the truth values true and false, usually denoted 1 and 0, respectively.

6) Tree : A tree is an acyclic graph or graph having no cycles. A tree or general trees is defined as a non-empty finite set of elements called vertices or nodes having the property that each node can have minimum degree 1 and maximum degree n.

7) Complete Graph : A complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction).

OR

A graph in which exactly one edge is present between every pair of vertices is called as a complete graph.

Q.2

(a) Explain types of a Relation with a suitable example.

The relations define the connection between the two given sets. Also, there are types of relations stating the connections between the sets.

'A set of ordered pairs is defined as a relation.’

• Empty Relation
  An empty relation (or void relation) is one in which there is no relation between any elements of a set. For example, if set A = {1, 2, 3} then, one of the void relations can be R = {x, y} where,
  |x – y| = φ. For empty relation,
  R = φ ⊂ ( A × A )
• Universal Relation
  A relation R in a set, say A is a universal relation if each element of A is related to every element of A, i.e., R = A × A. Also called Full relation. Suppose A is a set of all natural numbers and B is a set of all whole numbers. The relation between A and B is universal as every element of A is in set B. For universal relation,
  R = A × A
• Identity Relation
  In Identity relation, every element of set A is related to itself only. I = {(a, a), ∈ A}. For example, If we throw two dice, we get 36 possible outcomes, (1, 1), (1, 2), … , (6, 6). If we define a relation as R: {(1, 1), (2, 2), (3, 3), (4, 4), (5, 5), (6, 6)}, it is an identity relation.
  For identity relation,
  I = { (a, a) | a ∈ A }
• Inverse Relation
  Let R be a relation from set A to set B i.e., R ∈ A × B. The relation R-1 is said to be an Inverse relation if R-1 from set B to A is denoted by R-1 = {(b, a): (a, b) ∈ R}.Considering the case of throwing of two dice if R = {(1, 2), (2, 3)}, R-1 = {(2, 1), (3, 2)}. Here, the domain of R is the range of R-1 and vice-versa. So, for an inverse relation,
  R-1 = { (b, a) | (a, b) ∈ R}
• Reflexive Relation
  In a reflexive relation, every element maps to itself. For example, consider a set A = {1, 2,}. Now an example of reflexive relation will be R = {(1, 1), (2, 2), (1, 2), (2, 1)}. The reflexive relation is given by: (a, a) ∈ R
  OR
  If every element of set A maps to itself, the relation is Reflexive Relation.
  For every a ∈ A, (a, a) ∈ R.
• Symmetric Relation
  In a symmetric relation, if a=b is true then b=a is also true. In other words, a relation R is symmetric only if (b, a) ∈ R is true when (a,b) ∈ R. An example of symmetric relation will be R = {(1, 2), (2, 1)} for a set A = {1, 2}. So, for a symmetric relation,
  aRb ⇒ bRa, ∀ a, b ∈ A
  OR
  A relation R on a set A is said to be symmetric if (a, b) ∈ R then (b, a) ∈ R, for all a & b ∈ A.
• Transitive Relation
  For transitive relation, if (x, y) ∈ R, (y, z) ∈ R, then (x, z) ∈ R. For a transitive relation,
  aRb and bRc ⇒ aRc ∀ a, b, c ∈ A
  OR
  A relation in a set A is transitive if, (a, b) ∈ R, (b, c) ∈ R, then (a, c) ∈ R, for all a, b, c ∈ A.
• Equivalence Relation
  If a relation is reflexive, symmetric and transitive at the same time it is known as an equivalence relation.
  Define a relation R= {(a, b): a ∈ A, b ∈ B},
  we find that {(1, 1), (2, 2), …, (6, 6) ∈ R} (reflexive).
  If {(a, b) = (1, 2) ∈ R} then, {(b, a) = (2, 1) ∈ R} (symmetry).).
  If {(a, b) = (1, 2) ∈ R} and {(b, c) = (2, 3) ∈ R} then {(a, c) = (1, 3) ∈ R} (transitive).

(b) Rewrite the following statements using quantifier variables and

predicate symbols:

• All birds can fly.
• Some women are genius.
• There is a student who likes Discrete Mathematics but not Probability and Statistics.
• Each integer is either even or odd.

1) All birds can fly.

• Let B(x) be the predicate "x is a bird" and F(x) be the predicate "x can fly." The statement "All birds can fly" can be rewritten as:

∀ x [B(x) → F(x)]

2) Some women are genius.

• Let W(x) be the predicate "x is a woman" and G(x) be the predicate "x is a genius." The statement "Some women are genius" can be rewritten as:

∃ x [W(x) ^ G(x)]

3) There is a student who likes Discrete Mathematics but not Probability

and Statistics.

• Let S(x) be the predicate "x is a student," DM(x) be the predicate "x likes Discrete Mathematics," PS(x) be the predicate "x likes Probability and Statistics." The statement "There is a student who likes Discrete Mathematics but not Probability and Statistics" can be rewritten as:

∃ x [ S(x) ∧ DM(x) ∧ ¬PS(x) ]

4) Each integer is either even or odd

• Let I(x) be the predicate "x is an integer," E(x) be the predicate "x is even," and O(x) be the predicate "x is odd." The statement "Each integer is either even or odd" can be rewritten as:

∀x [ I(x) → ( E(x) ∨ O(x) ) ]

(C) Determine the validity of the argument given:

If I study, then I will not fail in Discrete Mathematics.

If I do not play cricket, then I will study. But I failed in Discrete Mathematics.

---

Therefore I must have played cricket.

• Above Statement is Valid

OR

(c) Find if the following is a tautology, contradiction or contingency.

(p → (q → r)) → ((p → q) → (p → r)).

p	q	r	q → r	p → (q → r)	p → q	p  → r	(p → q)→(p  → r)	R
T	T	T	T	T	T	T	T	T
T	T	F	F	F	T	F	F	T
T	F	T	T	T	F	T	T	T
T	F	F	T	T	F	F	T	T
F	T	T	T	T	T	T	T	T
F	T	F	F	T	T	T	T	T
F	F	T	T	T	T	T	T	T
F	F	F	T	T	T	T	T	T

All the entries in the last column(R) of the above truth table are T.

∴  (p →  (q → r)) → ((p → q) → (p  → r)) is a tautology.

Q.3

(a) Define: Bounded, Distributive and Complemented Lattices.

Complete Lattices :A complete lattice is a partially ordered set in which all subsets have both a Least Upper Bound (join) and an Greatest Lower Bound (meet).

Infinite lattice (Z,<=) is not complete lattice.

Bounded Lattices: A lattice L is called a bounded lattice if it has greatest element(1) and a least element (0).

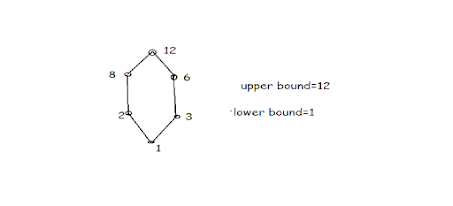
Here 12 (greatest element) is denoted as 1 (Least element) and 1 is denoted as 0.

Complemented Lattices:

A complemented lattice is a bounded lattice in which every element a has a complement

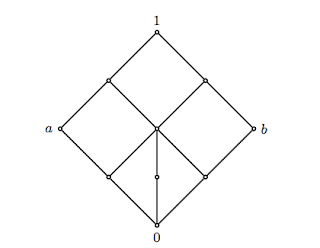
Here, Complement of 'a' is 'b' because, 'a' and 'b'  has a least element 0 and greatest element 1.

Distributive Lattices : A lattice L is called distributive lattice if for any elements a, b and c of L,it satisfies following distributive properties:

a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c)

a ∨ (b ∧ c) = (a ∨ b) ∧ (a ∨ c)

If the lattice L does not satisfies the above properties, it is called a non-distributive lattice.

Also , A lattice L is called distributive lattice if every element in L has atmost one complement.

For Example in Fig. of Bounded lattice, every element of Lettice has atmost 1 complement so lattice is called to be an distributive lattice.

(b) Find the transitive closure of

R = {(1,2), (3,4), (4,5), (4,1), (1,1)}. Where, A = {1,2,3,4,5}.

https://youtu.be/_-p8zhizock

(c) Let A be a set of factors of positive integer m and relation is divisibility

on A. For m = 45, show that POSET (A, ≤) is a Lattice.

A set id divisor of 45,

Therefore A= {1,3,5,9,15,45}

A= {(1, 1), (1, 3),(1,5),(1,9), (1, 15),

(1, 45),(3, 3), (3,9), (3, 15), (3, 45),

(5,5), (5, 15),(5, 45), (9,9), (9,45),

(15, 15), (15, 45), (45, 45)}

Hasse diagram :

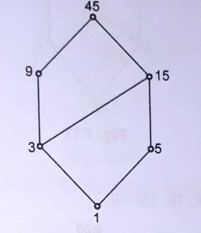
Table for join(Least Upper Bound) and meet(Greatest Lower Bound):

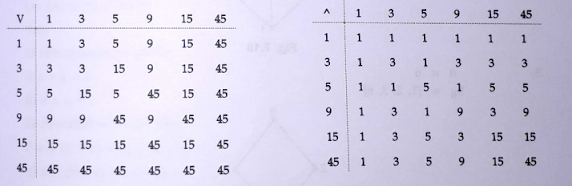
• Therefore Every pair has least upper bound and greatest lower bound, so it is a lattice.

OR

Ques 3

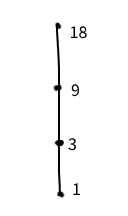
(a) Draw the Hasse diagram of the set {1,3,9,18} under partial order relation ‘divides’ and indicate those which are chains.

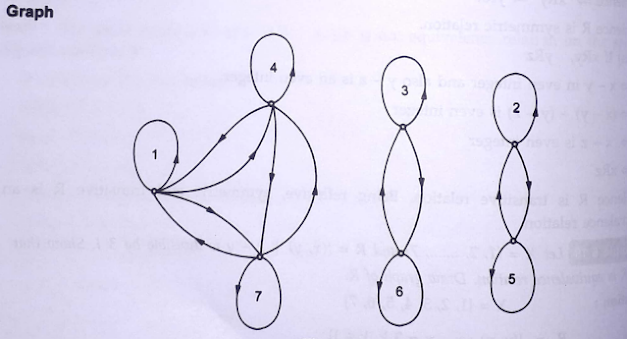
(b) Let X = {1,2,3, ... ,7} and R = {(x, y): x − y is divisble by 3}. Show

that R is an equivalence relation. Draw the graph of R.

X = {1, 2, 3, 4, 5, 6, 7}

R = (x-y ; = 3 k, k ∈  I}

(C) Solve the recurrence relation: $a$

Q.2

(a) Define group with example. Give an example of a non-abelian group.

Let G be a non-void set with a binary operation that assigns to each ordered pair (a, b) of elements of G an element of G denoted by a b.

We say that G is a group under the binary operation * if the following three properties are satisfied:

1) Associativity: The binary operation is associative i.e. a(bc)=(ab)*c , ∀ a,b,c ∈ G2) **Identity: There is an element e, called the identity, in G, such that ae=ea=a, ∀ a ∈ G3) **Inverse: For each element a in G, there is an element b in G, called an inverse of a such that a*b=b*a=e, ∀ a, b ∈ G

Example:

(I,+) is a group.

'+' is closure and associative operation on I.

Also 0 ∈  I

Such that 0 + a = a = a+0

And for all  a ∈ I , 3-a ∈ I

Such that a +(-a)= 0 = (-a) + a

Hence (I , +) is a group.

Example of a non-abelian group :

The group of the six permutations of the numbers 1, 2, 3 is the smallest non-abelian group. For example, the permutation (1 2), which swaps 1 and 2, does not commute with (1 3): Apply (1 2) first and then (1 3), that leads to the permutation (1 2 3) that rotates the three numbers (1 to 2, 2 to 3, 3 to 1).

(b) Let H = {[0],[3]} in Z6 under addition. Find left and right cosets in

<Z6, +6>.

To find the left and right cosets of the subgroup H = {[0],[3]} in Z₆ under addition, we need to consider all the possible cosets.

In general, the left cosets of a subgroup H in a group G are of the form gH, where g is an element of G. Similarly, the right cosets are of the form Hg. Here, Z₆ is the group and H is the subgroup.

Let's start by finding the left cosets:

Left coset 0 + H: 0 + {[0],[3]} = {[0],[3]}

Left coset 1 + H: 1 + {[0],[3]} = {[1],[4]}

Left coset 2 + H: 2 + {[0],[3]} = {[2],[5]}

Left coset 3 + H: 3 + {[0],[3]} = {[3],[0]}

Left coset 4 + H: 4 + {[0],[3]} = {[4],[1]}

Left coset 5 + H: 5 + {[0],[3]} = {[5],[2]}

Now, let's find the right cosets:

H + 0: {[0],[3]} + 0 = {[0],[3]}

H + 1: {[0],[3]} + 1 = {[1],[4]}

H + 2: {[0],[3]} + 2 = {[2],[5]}

H + 3: {[0],[3]} + 3 = {[3],[0]}

H + 4: {[0],[3]} + 4 = {[4],[1]}

H + 5: {[0],[3]} + 5 = {[5],[2]}

Therefore, the left cosets in Z₆ are: {[0],[3]}, {[1],[4]}, {[2],[5]}

And the right cosets in Z₆ are: {[0],[3]}, {[1],[4]}, {[2],[5]}

Note that in this case, the left and right cosets are the same since Z₆ is an abelian group (commutative), and addition is commutative.

(c) Prove that G = {1,2,3,4,5,6} is a finite abelian group of order 6 with

respect to multiplication modulo 7.

Since set is finite, we prepare the following multiplication table to examine the group axioms.

(G1)(G1) All the entries in the table are elements of G. Therefore G is closed with respect to multiplication modulo 7.

(G2)(G2) Multiplication modulo 7 is associative.

(G3)(G3) Since first row of the is identical to the row of elements of G in the horizontal border, the element to the left of first row in vertical border is identity element i.e., 1 is identity element in G with respect to multiplication mod 7.

(G4)(G4) From the table it is obvious that inverses of 1,2,3,4,5,6 are 1,4,5,2,3 and 6 respectively. Hence inverse of each element in G exists.

(G5)(G5) The composition is commutative because the elements equidistant from principal diagonal are equal each to each.

The set G has six element. Hence, (G,x7)(G,x7) is a finite abelian group of order 6.

Q.4

(a) Define subgroup and group Homomorphism.

In group theory, a branch of mathematics, given a group G under a binary operation ∗, a subset H of G is called a subgroup of G if H also forms a group under the operation ∗.

OR

A subgroup of a group G is a subset of G that forms a group with the same law of composition. For example, the even numbers form a subgroup of the group of integers with group law of addition.

A group homomorphism is a map between two groups such that the group operation is preserved: for all , where the product on the left-hand side is in and on the right-hand side in .

If (R,+) is a group of all real numbers under the operation ‘+’ & (R -{0},) is another group of non-zero real numbers under the operation ‘’ (Multiplication) & f is a mapping from (R,+) to (R -{0},*), defined as : f(a) = 2a ; ∀ a ∈ R

Then f is a homomorphism like – f(a+b) = 2a+b = 2a * 2b = f(a).f(b) .

So the rule of homomorphism is satisfied & hence f is a homomorphism.

(b) Is addition a binary operation on {-1,0,1}? Justify.

The sum of elements is (-1) + (-1) = -2 and 1+1=2 does not belong to A. Hence A is not closed under addition.

It forms group under condition of addition. Let G={-1,0,1} be non empty set with binary composition + from a group or satisfy addition operation on holding following conditions : 1+0=1€G,

• 1+1=0€G,
• 1+0=-1€G.

So G is closed under binary composition +

(c) Explain Cosets and Lagrange’s theorem.

Cosets : Let (G,) be a group and H be any subgroup of G. Let 'a' be any element of G.

Then the set

H a = (h a ; h E H} is called a right coset of H in G generated by a.

Similarly the set a H = (a * h ; h E H} is called a left coset of H in G.

Ha and a H are subsets of G.

Note: If G is an abelian group then H a = a H i.e. each right coset of H in G is also a left coset of H in G.

Lagrange theorem is one of the central theorems of abstract algebra. It states that in group theory, for any finite group say G, the order of subgroup H of group G divides the order of G. The order of the group represents the number of elements.

As per the statement, the order of the subgroup H divides the order of the group G. This can be represented as;

|G| = |H|

Proof of Lagrange Statement:

Let H be any subgroup of the order n of a finite group G of order m. Let us consider the cost breakdown of G related to H.

Now let us consider each coset of aH comprises n different elements.

Let H = {h1,h2,…,hn}, then ah1,ah2,…,ahn are the n distinct members of aH.

Suppose, ahi=ahj⇒hi=hj be the cancellation law of G.

Since G is a finite group, the number of discrete left cosets will also be finite, say p. So, the total number of elements of all cosets is np which is equal to the total number of elements of G. Hence, m=np

p = m/n

This shows that n, the order of H, is a divisor of m, the order of the finite group G. We also see that the index p is also a divisor of the order of the group.

Hence, proved, |G| = |H|

Q.5

(a) How many nodes are necessary to construct a graph with exactly 8 edges

in which each node is of degree 2.

Given-Number of edges = 24 And

Degree of each vertex = 4

Let number of vertices(nodes) in the graph = n.

Using Handshaking Theorem,

Sum of degree of all vertices = 2 x Number of edges

2 x n = 2 x 8n = 8

Thus, Number of vertices in the graph = 8.

(b) Find the shortest path between each pair of vertices for a simple digraph

using Warshall’s Algorithm.

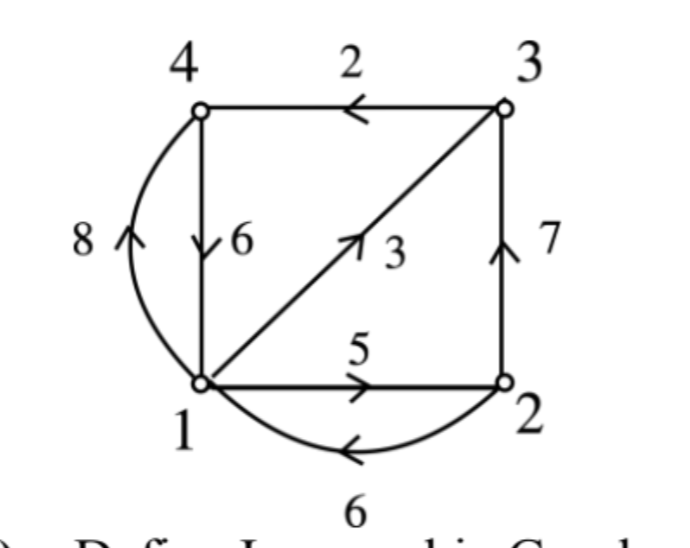
Follow the steps below to find the shortest path between all the pairs of vertices.

1. Create a matrix A0 of dimension n*n where n is the number of vertices. The row and the column are indexed as i and j respectively. i and j are the vertices of the graph. Each cell A[i][j] is filled with the distance from the ith vertex to the jth vertex. If there is no path from ith vertex to jth vertex, the cell is left as infinity.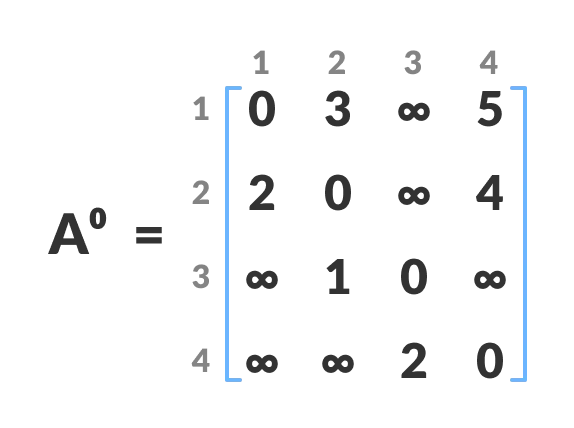
2. Now, create a matrix A1 using matrix A0. The elements in the first column and the first row are left as they are. The remaining cells are filled in the following way. Let k be the intermediate vertex in the shortest path from source to destination. In this step, k is the first vertex. A[i][j] is filled with (A[i][k]

   • A[k][j]) if (A[i][j] > A[i][k]

     • A[k][j]) . That is, if the direct distance from the source to the destination is greater than the path through the vertex k , then the cell is filled with A[i][k]
       • A[k][j].

     In this step, k is vertex 1. We calculate the distance from source vertex to destination vertex through this vertex k.

     

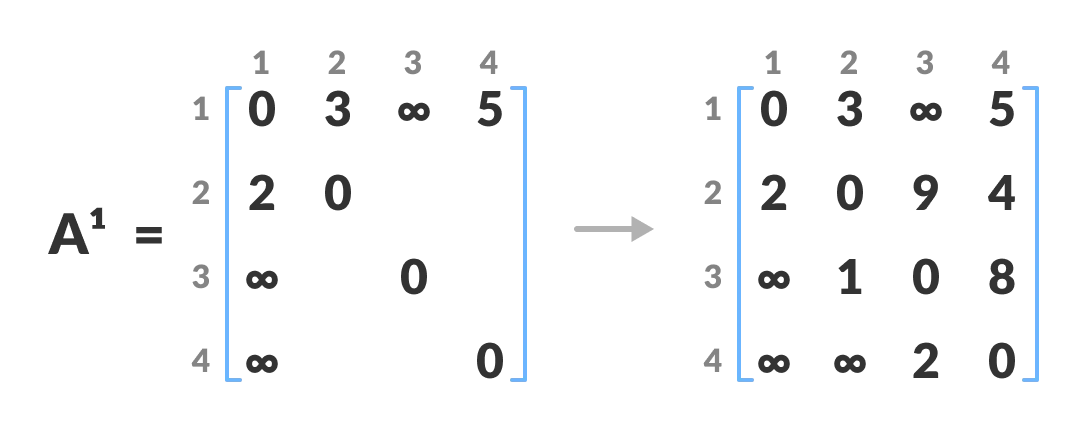
     For example: For A1[2, 4], the direct distance from vertex 2 to 4 is 4 and the sum of the distance from vertex 2 to 4 through vertex (ie. from vertex 2 to 1 and from vertex 1 to 4) is 7. Since 4 < 7, A0[2, 4] is filled with 4.

3. Similarly, A2 is created using A1 . The elements in the second column and the second row are left as they are. In this step, k is the second vertex (i.e. vertex 2). The remaining steps are the same as in step 2.
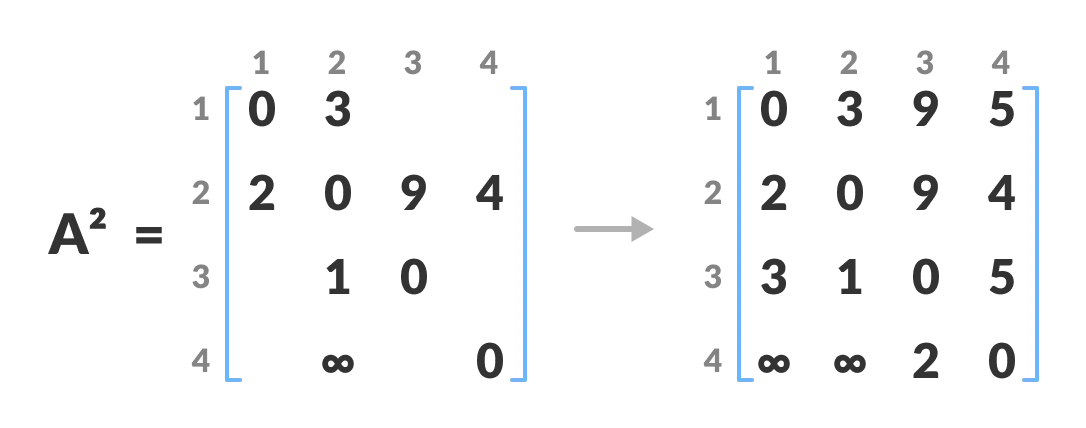
4. Similarly, A3 and A4 is also created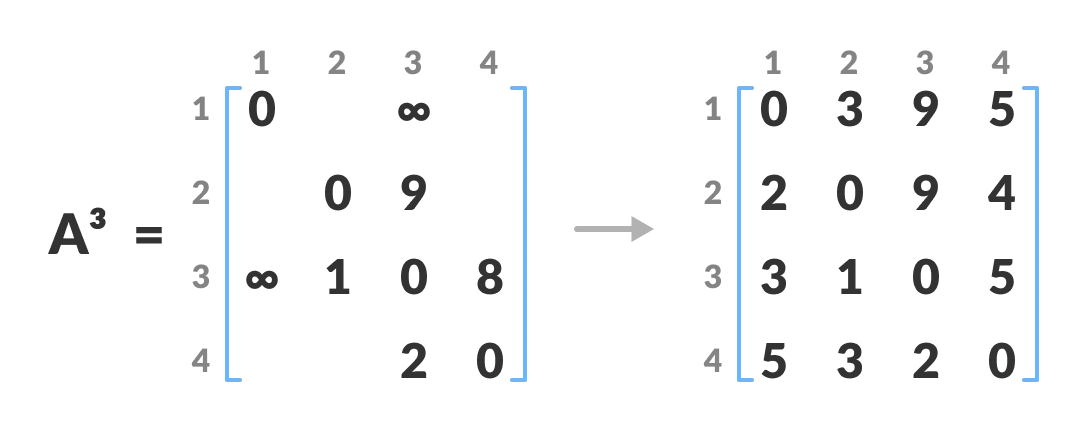

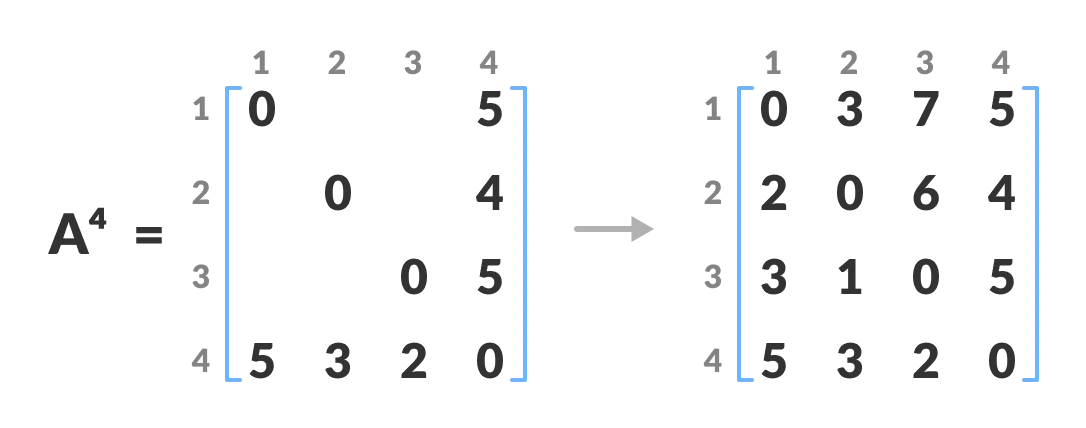
**A4 gives the shortest path between each pair of vertices.

(c) Define Isomorphic Graphs. Verify the following graphs are Isomorphic

or not (Justify).

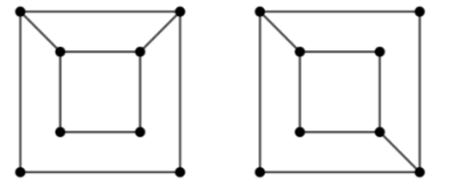
Graph Isomorphism is a phenomenon of existing the same graph in more than one forms. Such graphs are called as Isomorphic graphs.

For any two graphs to be isomorphic, following 4 conditions must be satisfied-

• Number of vertices in both the graphs must be same.
• Number of edges in both the graphs must be same.
• Degree sequence of both the graphs must be same.
• If a cycle of length k is formed by the vertices { v1 , v2 , ….. , vk } in one graph, then a cycle of same length k must be formed by the vertices { f(v1) , f(v2) , ….. , f(vk) } in the other graph as well.

The following conditions are the sufficient conditions to prove any two graphs isomorphic :

• Two graphs are isomorphic if and only if their complement graphs are isomorphic.
• Two graphs are isomorphic if their adjacency matrices are same.
• Two graphs are isomorphic if their corresponding sub-graphs obtained by deleting some vertices of one graph and their corresponding images in the other graph are isomorphic.

Are following Graph Isomorphic ?

solution :

Condition-01:

• Number of vertices in graph G1 = 8
• Number of vertices in graph G2 = 8

Here,

• Both the graphs G1 and G2 have same number of vertices.
• So, Condition-01 satisfies.

Condition-02:

• Number of edges in graph G1 = 10
• Number of edges in graph G2 = 10

Here,

• Both the graphs G1 and G2 have same number of edges.
• So, Condition-02 satisfies.

Condition-03:

• Degree Sequence of graph G1 = { 2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 }
• Degree Sequence of graph G2 = { 2 , 2 , 2 , 2 , 3 , 3 , 3 , 3 }

Here,

• Both the graphs G1 and G2 have same degree sequence.
• So, Condition-03 satisfies.

Condition-04:

• In graph G1, degree-3 vertices form a cycle of length 4.
• In graph G2, degree-3 vertices do not form a 4-cycle as the vertices are not adjacent.

Here,

• Both the graphs G1 and G2 do not contain same cycles in them.
• So, Condition-04 violates.

Since Condition-04 violates, so given graphs can not be isomorphic.

∴ G1 and G2 are not isomorphic graphs.

OR

Q.5

(a) Define Cyclic graph, Null graph and Strongly connected graph.

1. Cyclic graph:

A simple graph of ‘n’ vertices (n>=3) and n edges forming a cycle of length ‘n’ is called as a cycle graph. In a cycle graph, all the vertices are of degree 2.

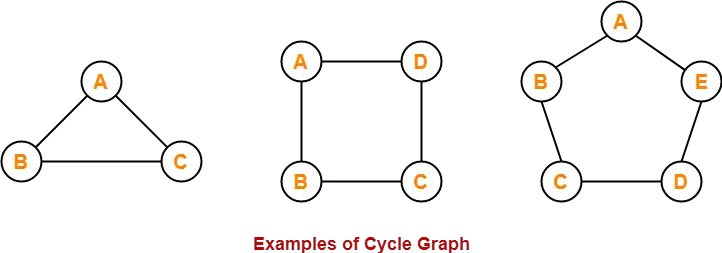
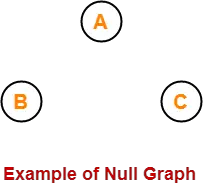
2. Null graph:

• A graph whose edge set is empty is called as a null graph.
• In other words, a null graph does not contain any edges in it.
  

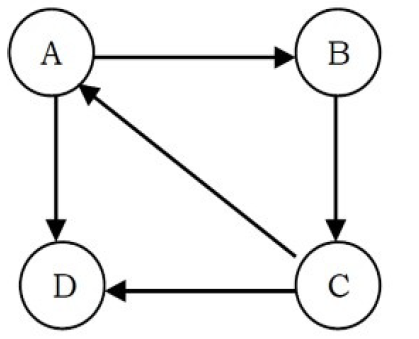
3. Strongly connected graph : A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first.

when there is a path between each pair of vertices in one component.

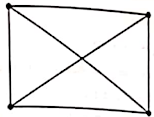
(b) Draw a graph which is regular but not bipartite.

A graph is said to be regular or K-regular if all its vertices have the same degree K. OR a bipartite graph is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the parts of the graph.

(c) For the following set of weights construct an optimal binary prefix code.

For each weight in the set, give corresponding code word. 5, 7, 8, 15, 35, 40

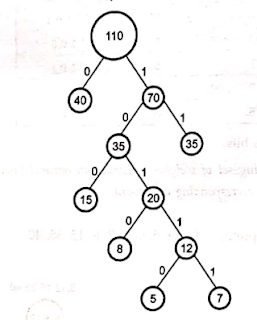
Code for 7 : 10111 Code for 8 : 1010 Code for 15 : 100 Code for 35 : 11 Code for 40 : 0