Ai Summer 2023 Previous Year Paper Solutions 3161608

Q1

A. Define artificial intelligence. List the task domain of artificial intelligence with an example. (3 marks)

Aritificial Intelligence is a way of making computer or computer controlled robot or software that can act intelligently in similar manner as human can act.

Task Domain of AI:

There are various task domain in which Ai is used and they are as follows :

1. Machine Learning (ML): Machine learning is a way of teaching machines to learn from data.
2. Natural Language processing (NLP): NLP is all about teaching machines or robots to communicate and understand in human languages.
3. Computer Vision (CV) : AI can also be used in computer vision for recognizing and identifying patterns, objects, people and even emotions from image or video.
4. Robotics: It is all about creating machines that can perform physical task and mimic human movements and actions.

In summary, we can say that AI can be used for learning and communicating, see and interacting with the world like human intelligence.

B. Differentiate between best first search and breadth first search. (4 marks)

Best First Search	Breadth First Search
It can be implemented using Queue sorted by heuristic function.	It can be implement using FIFO data structure.
Completeness: It is incomplete strategy. It is based on heuristic function.	Completeness: It is complete strategy
Optimality: It is basically not optimal, even though It is based on heuristic function	Optimality: It is optimal strategy
Memory Requirement: It requires high memory usage.	Memory Requirement: It also requires high memory usage.
use cases: suited for complex problems	use cases: suited for small problems
time complexity: O(b^m)	time complexity: O(b^d)
space complexity: O(b^m)	space complexity: O(b^d)

C. Explain Alpha-Beta cutoff procedure in game playing with example. (7 marks)

Alpha-beta pruning

• Alpha beta pruning is modified version of min-max concept and optimize the efficieny.
• As we have seen in the minimax search algorithm that the number of game states it has to examine are exponential in depth of the tree. Since we cannot eliminate the exponent, but we can cut it to half. Hence there is a technique by which without checking each node of the game tree we can compute the correct minimax decision, and this technique is called pruning. This involves two threshold parameter Alpha and beta for future expansion, so it is called alpha-beta pruning. It is also called as Alpha-Beta Algorithm.
• Alpha-beta pruning can be applied at any depth of a tree, and sometimes it not only prune the tree leaves but also entire sub-tree.
• Alpha-beta pruning introduces two threshold parameter for future expansion and they are alpha and beta and thats why it’s called alpha-beta pruning.

Threshold parameters

• Alpha-beta pruning introduces two threshold parameters for future expansion and they are as follows:
  • Alpha(α) : It is best highest value of maximizer and initial value of α is -α
  • Beta (β) : It is the best lowest value of minimizer and initial value of β is +β

Condition: for Alpha beta pruning is α ≥ β

Example :

Let's take an example of two-player search tree to understand the working of Alpha-beta pruning

Step 1: At the first step the, Max player will start first move from node A where α= -∞ and β= +∞, these value of alpha and beta passed down to node B where again α= -∞ and β= +∞, and Node B passes the same value to its child D.

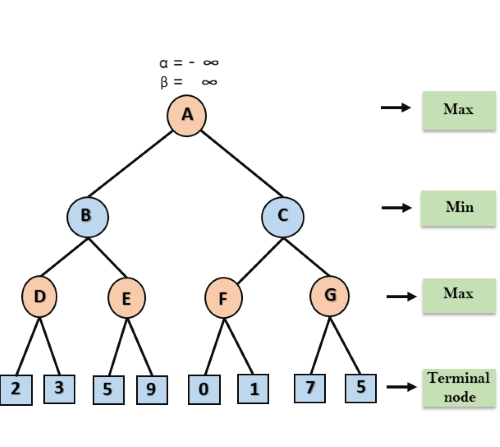
Step 2: At Node D, the value of α will be calculated as its turn for Max. The value of α is compared with firstly 2 and then 3, and the max (2, 3) = 3 will be the value of α at node D and node value will also 3.

Step 3: Now algorithm backtrack to node B, where the value of β will change as this is a turn of Min, Now β= +∞, will compare with the available subsequent nodes value, i.e. min (∞, 3) = 3, hence at node B now α= -∞, and β= 3.

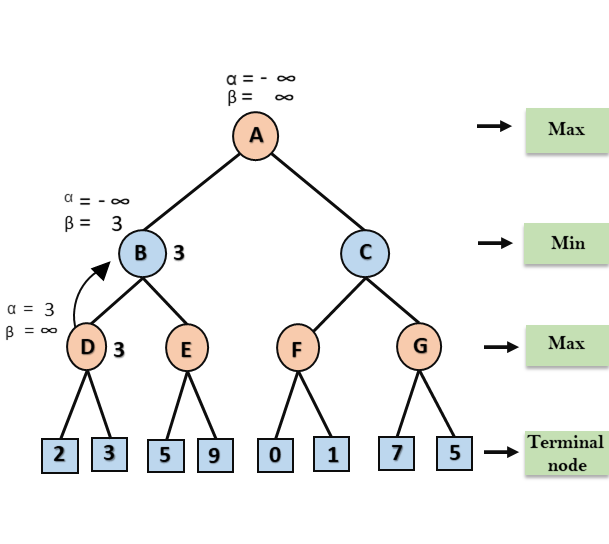
In the next step, algorithm traverse the next successor of Node B which is node E, and the values of α= -∞, and β= 3 will also be passed.

Step 4: At node E, Max will take its turn, and the value of alpha will change. The current value of alpha will be compared with 5, so max (-∞, 5) = 5, hence at node E α= 5 and β= 3, where α>=β, so the right successor of E will be pruned, and algorithm will not traverse it, and the value at node E will be 5.

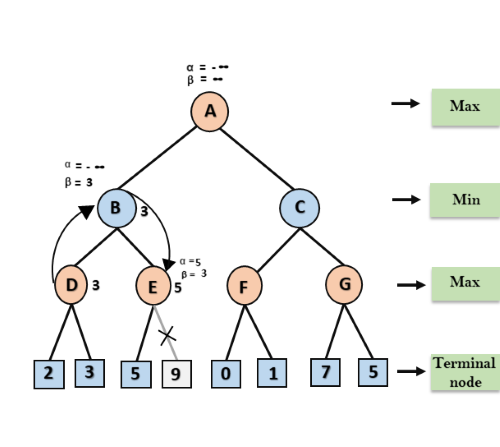
Step 5: At next step, algorithm again backtrack the tree, from node B to node A. At node A, the value of alpha will be changed the maximum available value is 3 as max (-∞, 3)= 3, and β= +∞, these two values now passes to right successor of A which is Node C.

At node C, α=3 and β= +∞, and the same values will be passed on to node F.

Step 6: At node F, again the value of α will be compared with left child which is 0, and max(3,0)= 3, and then compared with right child which is 1, and max(3,1)= 3 still α remains 3, but the node value of F will become 1.

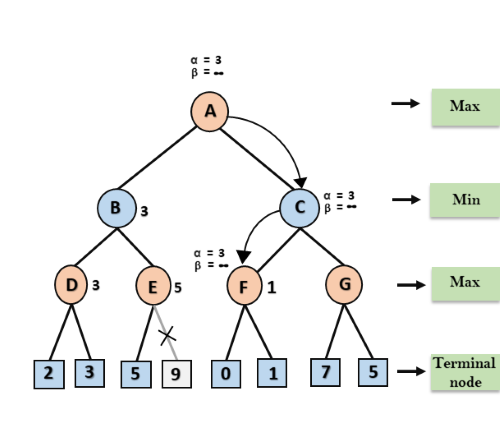
Step 7: Node F returns the node value 1 to node C, at C α= 3 and β= +∞, here the value of beta will be changed, it will compare with 1 so min (∞, 1) = 1. Now at C, α=3 and β= 1, and again it satisfies the condition α>=β, so the next child of C which is G will be pruned, and the algorithm will not compute the entire sub-tree G.

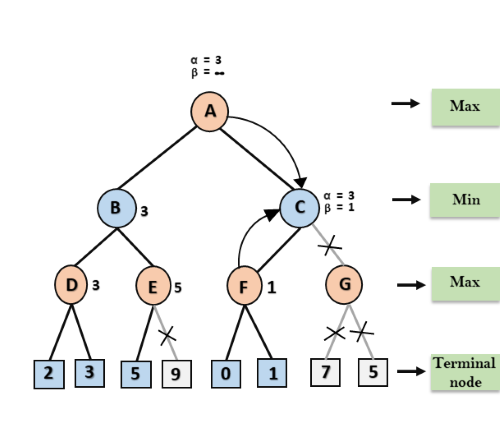
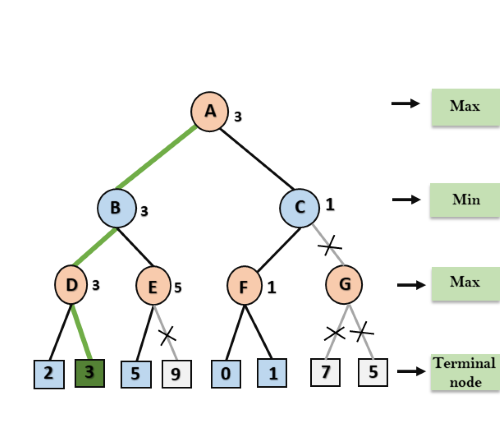
Step 8: C now returns the value of 1 to A here the best value for A is max (3, 1) = 3. Following is the final game tree which is the showing the nodes which are computed and nodes which has never computed. Hence the optimal value for the maximizer is 3 for this example.

Advantages

• The simple min-max concept can really slow-down for the complex games such as chess.
• So , Alpha Beta pruning is improved version that is used for overcoming this problems.

Q2

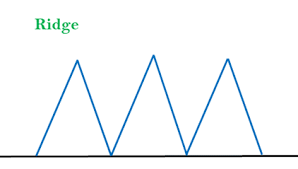
(a) Explain: (i) Local maximum (ii) Plateau (iii) Ridge (3 marks)

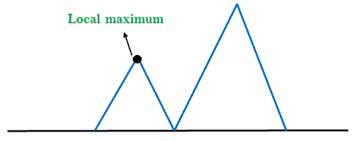
1. Local Maximum: is a peak state in state space diagram. it defines that it is better than all of its neighbouring states

   

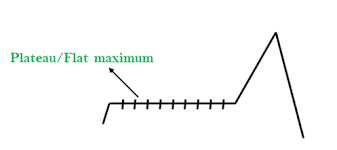
2. Plateau: It is a flat area in state space diagram, in this plateau the neighbouring states of its current state contains same value.

   

3. Ridges: It is a special form of local maximum which defines the highest value of its all neighbouring states.

   

(b) Discuss Goal Stack Planning. (4 marks)

Goal Stack Planning is one of the earliest methods in artificial intelligence in which we work backwards from the goal state to the initial state.

We start at the goal state and we try fulfilling the preconditions required to achieve the initial state. These preconditions in turn have their own set of preconditions, which are required to be satisfied first.

We keep solving these “goals” and “sub-goals” until we finally arrive at the Initial State. We make use of a stack to hold these goals that need to be fulfilled as well the actions that we need to perform for the same.

Apart from the “Initial State” and the “Goal State”, we maintain a “World State” configuration as well. Goal Stack uses this world state to work its way from Goal State to Initial State. World State on the other hand starts off as the Initial State and ends up being transformed into the Goal state.

Given below are the list of predicates as well as their intended meaning

1. ON(A,B) : Block A is on B
2. ONTABLE(A) : A is on table
3. CLEAR(A) : Nothing is on top of A
4. HOLDING(A) : Arm is holding A.
5. ARMEMPTY : Arm is holding nothing

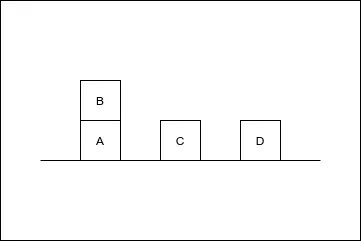
Initial state

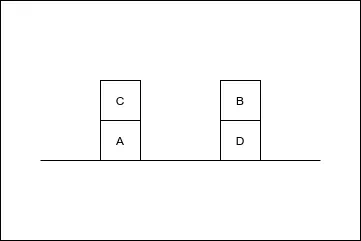
Goal state

(c) Explain AO* algorithm. (7 marks)

AO Algorithm Explanation

• AO Algorithm, or And/Or graph heuristic search algorithm, is an advanced form of heuristic search designed to handle decision processes with multiple agents and complex goal structures, unlike the more linear A algorithm.
  • It is used for solving problems modeled as acyclic and/or graphs, optimizing the solution by evaluating all possible subproblems or subgoals.
• Like A Algorithm, AO uses heuristic estimates to evaluate the node's potential, focusing on the cost to reach a goal state through the most promising path.

Working of AO Algorithm

• The working of the AO* Algorithm can be visualized in a diagram representing an and/or graph where nodes represent states and edges represent actions.

Algorithm

1. Begin by identifying the initial node and evaluate its heuristic.
2. Check if the initial node is a goal node; if it is, terminate the search.
3. Select a node for expansion based on a heuristic function that evaluates the cheapest cost to achieve the goal, prioritizing nodes that could directly or indirectly satisfy the goal.
4. Expand the selected node into its successors. In an and/or graph, these could be either conjunctions (AND nodes that require all child nodes to be solved) or disjunctions (OR nodes that require at least one child node to be solved).
5. For each successor, calculate the heuristic value and update the cost estimate of reaching the goal from the initial node.
6. Update the graph structure, marking nodes as solved if their conditions (all children for AND, at least one child for OR) are met.
7. Repeat the process from step 2 until the entire graph is evaluated or the goal is achieved.

Advantages

• AO* Algorithm is goal-directed and highly efficient for structured problems with clear sub-goals.
• It can effectively handle both conjunctive (AND) and disjunctive (OR) conditions in problem-solving.
• Optimizes processing by focusing on the most promising paths through heuristic evaluation, similar to A*.

Disadvantages

• Like A, the AO Algorithm is heavily dependent on the accuracy of the heuristic function, which can limit its effectiveness if the heuristic is poorly defined.
• AO* requires significant memory and computational resources, especially for large and complex graphs with many nodes and edges.
• The algorithm's performance can degrade if the graph structure involves a lot of re-evaluations due to interdependencies between nodes.

OR

(c) Explain A* algorithm. (7 marks)

• A* Algorithm is most important and commonly known special form of Best First Search (BFS) Algorithm.
• It finds the solution as shortest path by finding the state space tree by heuristic problem.
• A* Algorithm is similar as UTS because it uses f(n) + g(n) instead of using only f(n).

Working of A* Algorithm

• working of A* Algorithm can be described as follows: $f(n) = g(n) + h(n)$
  • where f(n) is estimated cost, g(n) is cost to reach the ‘n’ node from initial node [evaluation function], h(n) is cost to reach goal node from ‘n’ node

Algorithm

1. Starting by placing the start node in open list.
2. Check whether openlist is empty or not if it is empty then returns.
3. select the node from openlist which has the smallest value of evaluation function and if it is goal state then returns.
4. expand the node in to its successors and they are part of openlist and close list then return and place the node in closed list.
5. Calculate the evaluation function of successor ni, and place in to open list.
6. repeat from step 2.

Advantages

• It is complete and optimal.
• It can solve any complex problem easily.
• A* Algorithm is best algorithm from all searching strategies.

Diadvantages

• Main drawback of A* is memory requirement.
• A* Algorithm does not give gaurantee of finding the optimal solution.
• A* algorithm has some complexity issues.

Q3

(a) Describe different heuristics for the Blocks world problem. (3 marks)

Heuristic function is a function that is used in informed search for finding promixing path.

Heuristic function can be represented as follows:

$h(n) = h'(n)$

where h(n) is heuristic and h’(n) is actual cost.

Heuristic function takes the current state as an input and provides estimation of cost.

Heuristic function can not give the gaurantee of best solution but it provides always good solution in reasonable time.

(b) Differentiate propositional logic and predicate logic. (4 marks)

Propositional Logic	Predicate logic
Propositional logic is simplest form of logic in which statements are made up by propositions	Predicate logic represents logical construct that specifies rule or condition
It is very basic and generally used that’s why it is called boolean logic	Predicate logic are extension of propositions

| It specifies the truth value that must be

eirther be true or false. | It specifies the truth value which depends on the variable value. |

| propositons are connected by the logical connectives. | predicates introduces quantifiers to existing statement. |

| It is more generalized representation | It is more specialized representation |

| It can not deal with set of entities | It can deal with the set of entities |

(c) Solve the following Cryptarithmetic Problem. (7 marks)

SEND

+MORE

---

MONEY

In thsi example, we can take the value of D is 7, value of N is 6, value of E is 5, value of S is 9, value of M is 1, value of O is 0, value of R is 8, and value of E is 5.

so we can write is as following:

9 5 6 7 +1 0 8 5 ———— 1 0 6 5 2

OR

Q3

(a) Explain Unification. (3 marks)

Unification is a process where two logical expressions are made identical by finding a substitution for variables.

It involves recursively matching corresponding components of the expressions, allowing variables to be instantiated with terms, and determining if the expressions can be unified.

Unification is fundamental in languages like Prolog for pattern matching, goal resolution, and constraint solving, enabling the execution of programs by determining if goals can be satisfied based on the available knowledge.

(b) Discuss Bay’s theorem. (4 marks)

Bayes' Theorem is a fundamental theorem that describes the probability of an event based on prior knowledge or beliefs about related events.

It provides a mathematical framework for updating probabilities as new evidence becomes available.

The theorem is often used in various fields, including statistics, machine learning, and artificial intelligence.

It is a way to calculate the value of P(B|A) with the knowledge of P(A|B).

Bayes' Theorem is expressed as:

$P(A|B) = \frac{P(B|A)*P(A)}{P(B)}$

Where:

• 𝑃(𝐴∣𝐵)P(A∣B) is the posterior probability of event A given evidence B.
• 𝑃(𝐵∣𝐴)P(B∣A) is the likelihood of evidence B given that A is true.
• 𝑃(𝐴)P(A) is the prior probability of event A.
• 𝑃(𝐵)P(B) is the prior probability of evidence B.

Key points about Bayes' Theorem:

1. Updating Probabilities
2. Prior and Posterior Probabilities
3. Likelihood
4. Normalization
5. Application

Example : what is the probability that a patient has diseases meningitis with a stiff neck?

A doctor is aware that disease meningitis causes a patient to have a stiff neck, and it occurs 80% of the time. He is also aware of some more facts, which are given as follows:

• The Known probability that a patient has meningitis disease is 1/30,000.
• The Known probability that a patient has a stiff neck is 2%.

Let a be the proposition that patient has stiff neck and b be the proposition that patient has meningitis. , so we can calculate the following as:

P(a|b) = 0.8

P(b) = 1/30000

P(a)= .02

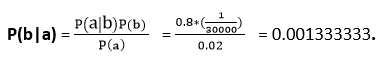
Hence, we can assume that 1 patient out of 750 patients has meningitis disease with a stiff neck.

(c) Consider the following sentences: (7 marks)

• John likes all kinds of food. • Apples are food. • Chicken is food. • Anything anyone eats and isn’t killed by is food. • Bill easts peanuts and is still alive.

• Sue eats everything Bill eats.

(i) Translate these sentences into formulas in predicate logic.

1. Let Likes(x,y) be a predicate representing that person x likes item y.
2. Let Food(x) be a predicate representing that item x is food.

From the given sentences, we can form the following predicate logic formulas:

• John likes all kinds of food: ∀x(Food(x)→Likes(John,x))
• Apples are food: Food(apples)
• Chicken is food: Food(chicken)
• Anything anyone eats and isn’t killed by is food: ∀x∀y (Eats(y,x) ∧ Alive(y) → Food(x))
  • Eats(x,y): person x eats item y.
  • Alive(x): person x is still alive after eating.
• Bill eats peanuts and is still alive: Eats(Bill,peanuts)∧Alive(Bill)
• Sue eats everything Bill eats: ∀x(Eats(Bill,x)→Eats(Sue,x))

(ii) Prove that John likes peanuts using backward chaining.

1. Goal: Likes(John,peanuts)
2. From formula 1 (∀x(Food(x)→Likes(John,x))), we need to prove Food(peanuts) to satisfy Likes(John,peanuts).
3. To prove Food(peanuts), we use formula 4 (∀x∀y(Eats(y,x)∧Alive(y)→Food(x))).
4. We need instances where Eats(y,peanuts) and Alive(y) hold.
5. From formula 5, we know Eats(Bill,peanuts)∧Alive(Bill) is true.
6. Applying formula 4 with y=Bill and x=peanuts, it follows that Food(peanuts) is true since Eats(Bill,peanuts)∧Alive(Bill).
7. With Food(peanuts) established, by formula 1, Likes(John,peanuts) is true.

Thus, by backward chaining, we can conclude that John likes peanuts. This proof follows from the logical deductions based on the provided rules and statements.

Q4

(a) Explain AND-OR graphs. (3 marks)

AND - OR Graphs:

AO* Algorithm is used for complex problems that can be decomposible in to smaller subproblems and that can be easily solved by AND-OR graphs.

AND OR Graphs are specialized graphs that is used for complex problems to make them more manageable in order to find the solution.

AND OR Graphs are specialized graphs in which AND portion of graph represents the set of tasks for achieving the goals, OR portion of graph represents the different methods for accomplishing the same goal.

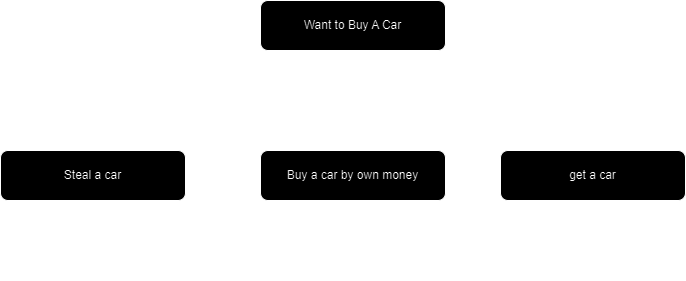
In the above example statement ‘steal a car’ includes the OR portion. AND Portion includes two statements and they are ‘buy a car with own money’ and ‘get a car’.

Working of AO* Algorithm:

Explanation :

F(n) = g(n) + h(n)

where g(n) is actual cost, h(n) is estimated cost.

[ Evaluation function ]

(b) Explain depth first search algorithm. (4 marks)

Depth First Search (DFS) is recursive and backtracking algorithm for traversing a graph or tree.

Working:

The working of Depth First Search is similar to the Breadth First Search.

Search Order:

DFS is implemented using stack data-structure, it uses FIFO (First in First out) strategy, so the search order is FIFO.

DFS Traverses the graph by fully exploring the node by expanding its children recursively until the end is reached only after then moving to the next node.

Advantages:

The main advantage of Depth First Search is to require less memory because it only needs to store stack of nodes.

It also requires less time so that it is faster than BFS.

Disadvantages:

The disadvantage of Depth-First Search is that there is a possibility that it may down the left-most path forever. Thus it may get stuck in infinite loop.

It does not give the gaurantee of finding the optimal solution.

Time Complexity:

O (b^d)

where b is current state of node, d is depth of tree.

Space Complexity:

O (b^d)

where b is current state of node, d is depth of tree.

Example:

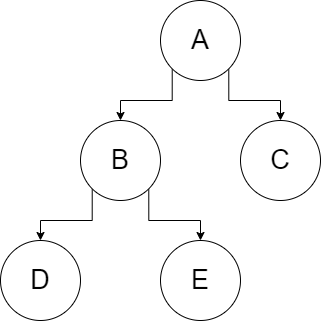
Solution Search Order:

A B D E C

(c) Explain forward and backward reasoning with example. (7 marks)

Forward and Backward Reasoning:

Forward and Backward reasoning are two important strategies that is used in field of AI and lies in Expert system domain of AI.

Forward and Backward Reasoning are used by inference Engine for making deductions.

Forward chaining

Definition :

• In Forward Reasoning, the inference engine goes through all facts and conditions before deducing the outcomes.
• When data is available and than decision is taken, this process is called “Forward Chaining”.

Direction :

• It works in forward direction that means it starts from the initial state and reached to the goal state.

Example:

A A→B B ——————————— Statement A: It is raining. Statement A→B: It is raining, then street is wet. Statement B: street is wet.

Backward Reasoning

Definition:

• In Backward reasoning, inference engine knows about the information of goal or goal state so that it starts from goal state and works backend in direction.

Direction:

• It works in backward direction, so that it starts from the goal state and reached to the initial state.

Example:

B A→B A ———————— Statement B : The street is wet Statement A → B: if it is raining the street is wet Statement A: It is raining.

Difference between Forward and Backward Reasoning.

Forward Reasoning	Backward Reasoning
It is known as data-driven approach.	It is known as goal-driven approach.
Bottom up approach.	Top Down approach.
The goal is to get the conclusion	The goal is to get required information
Applies Breadth first search	Applies Depth first search

OR

Q4

(a) Discuss limitations of Hill climbing search method. (3 marks)

Hill climbing is a local search algorithm used in problem-solving and optimization tasks. While it has certain advantages, it also has several limitations:

1. Local Optima: Hill climbing tends to get stuck in local optima, where it reaches a solution that is optimal in its local neighborhood but may not be the global optimum. It lacks the capability to backtrack and explore other regions of the search space.
2. Plateaus: When faced with flat regions or plateaus in the search space where all neighboring states have the same value, hill climbing struggles to make progress. It may oscillate or get stuck in such regions, leading to inefficiency.
3. Greedy Approach: Hill climbing adopts a greedy strategy by always selecting the best neighboring state without considering the long-term consequences. This myopic view can lead to suboptimal solutions, especially in problems where local improvements do not necessarily lead to global improvements.
4. Initialization Dependency: The performance of hill climbing can be heavily dependent on the initial state from which it starts the search. A poor initial state may lead to premature convergence or failure to find a satisfactory solution.
5. Limited Memory: Hill climbing typically has limited memory and does not maintain a history of visited states. This limits its ability to backtrack and explore alternative paths, especially in complex search spaces.

(b) Is the minimax procedure a depth-first or breadth-first search procedure? Explain. (4 marks)

The minimax procedure is primarily a depth-first search (DFS) procedure, although it incorporates elements of breadth-first search (BFS) as well. Let's discuss why minimax is considered primarily a DFS procedure:

1. Depth-First Search (DFS) Nature:
   • Minimax explores the game tree in a depth-first manner, starting from the root node (initial game state) and recursively exploring each branch until a terminal state (end of the game) is reached.
   • At each level of the tree, minimax evaluates the possible moves (successor states) and selects the best move based on the current player's perspective (maximizing or minimizing).
2. Depth-First Traversal:
   • In minimax, the search proceeds by deeply exploring one branch of the game tree at a time, rather than exploring all possible moves at each level simultaneously.
   • This depth-first traversal allows minimax to efficiently explore deeper levels of the tree, focusing on promising paths that lead to potential optimal solutions.
3. Backtracking:
   • As minimax traverses deeper into the game tree, it backtracks to previously explored nodes once a terminal state or a specified depth limit is reached.
   • Backtracking is a characteristic feature of depth-first search algorithms, allowing them to explore alternative paths when necessary.
4. Pruning Techniques:
   • Minimax often incorporates alpha-beta pruning, a technique used to reduce the number of nodes evaluated during search by eliminating branches that are known to be suboptimal.
   • Alpha-beta pruning is most effective in depth-first traversal, as it exploits the recursive nature of the search to prune subtrees that cannot affect the final decision.

While minimax primarily follows a depth-first search strategy, it also exhibits some characteristics of breadth-first search, particularly when it comes to evaluating and comparing moves at each level of the game tree. However, the fundamental approach of exploring one path deeply before considering alternatives aligns it more closely with the depth-first search paradigm.

(c) Discuss the different approaches to knowledge representation. (7 marks)

Knowledge representation is a fundamental concept in artificial intelligence (AI) and cognitive science, aiming to capture, organize, and manipulate knowledge in a form that computers can understand and reason with. There are several approaches to knowledge representation, each with its own strengths and weaknesses:

1. Semantic Networks:
   • Semantic networks represent knowledge as a network or graph structure, where nodes represent concepts or entities, and edges represent relationships between them.
   • They are intuitive and easy to understand, making them suitable for modeling hierarchical and relational knowledge.
   • However, they can become complex and unwieldy for large knowledge bases, and the semantics of the relationships may be ambiguous.
2. Frames:
   • Frames are a structured representation technique that organizes knowledge into units called frames, which consist of slots for properties and values.
   • Frames are particularly useful for representing structured knowledge about objects, events, or concepts, allowing for inheritance, default values, and slot-filling.
   • However, they may struggle with representing complex relationships and may require extensive encoding for nuanced knowledge.
3. Rule-based Systems:
   • Rule-based systems represent knowledge in the form of if-then rules, where conditions trigger actions or inferences.
   • They are expressive and can capture complex logical relationships and reasoning processes.
   • However, managing and maintaining a large set of rules can be challenging, and rule interactions may lead to unintended consequences or conflicts.
4. Logic-based Representations:
   • Logic-based representations, such as predicate logic and first-order logic, use formal logical languages to express knowledge in terms of facts, rules, and queries.
   • They provide a precise and unambiguous representation of knowledge, suitable for automated reasoning and inference.
   • However, expressing certain types of knowledge, such as uncertainty or probabilistic information, may be difficult in pure logic.
5. Ontologies:
   • Ontologies represent knowledge using a formal vocabulary of concepts, relations, and axioms, organized in a hierarchical structure.
   • They aim to provide a shared and standardized vocabulary for a specific domain, facilitating interoperability and knowledge sharing.
   • Ontologies are widely used in areas such as the Semantic Web, where they enable automated reasoning and intelligent information retrieval.
6. Connectionist or Neural Networks:
   • Connectionist models represent knowledge as distributed patterns of activation in interconnected nodes, inspired by the structure and function of the brain.
   • They excel at learning from data and can capture complex patterns and relationships through training.
   • However, they are often considered black boxes, making it difficult to interpret or extract explicit knowledge from them.

Each approach to knowledge representation has its own strengths and weaknesses, and the choice of representation depends on factors such as the nature of the problem domain, the requirements of the application, and the capabilities of available computational resources. Hybrid approaches that combine multiple representation techniques are also common, leveraging the strengths of each approach to overcome their individual limitations.

Q5

(a) Discuss in brief the Hopfield network? (3 marks)

HOPField Network

Invention : Hopfield neural network was invented by John J Hopfield, and it consists of one layer of ‘n’ fully connected recurension neurals.

Application : Hopfiel dneural network is used for performing auto-associated and optimization operations.

Discrete Hopfield Neural Network :

• Discrete hopfield neural network is n fully interconnected neural network in which each unit is connected to each other unit.
• this hopfield behaves in discrete manner and provides finite number of distinct output which has following types: 1. Binary (0/1) 2. Bipolar (-1/1)

Nature:

• The weight associated with neural network is symmetric in nature and also have following properties and they are as follows :

1. w ij = w ji
2. wii = O

(b) Discuss Bayesian network with and application. (4 marks)

Bayesian belif network is graphical representation of different probabilistic relationship of random inputs of a particular set.

Bayesian Belif network is classifier with no dependency on attributes.

Applications :

1. System Biology
2. Biomonitoring
3. medical industry
4. document classification
5. span filter
6. semantic search
7. information retrieval
8. image processing
9. turbo code

Example:

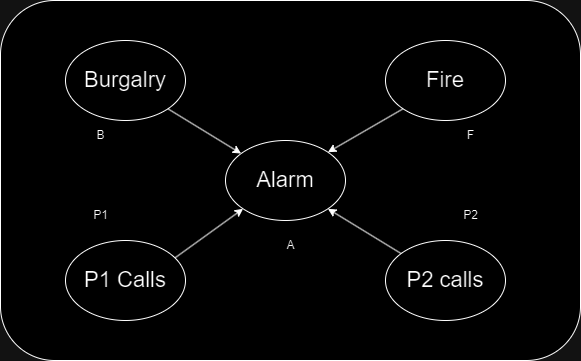
• In above example, there is an Alarm (A) that has been installed in a house.
• Which rangs upon two probability [B] and [F] and Burgarly and Fire are parent nodes of the Alarm [A]
• and Alarm [A] is parent nodes of two probabilities (p1 calls) and (p2 calls)

Overall, Bayesian belif network provides the feature of full joint probability and probability among this network based on conditions.

(c) Write following Prolog programs: (7 marks)

(i) To find the maximum number from the three numbers.

% Define a rule to find the maximum of two numbers
max(X, Y, X) :- X >= Y.
max(X, Y, Y) :- X < Y.

% Define a rule to find the maximum of three numbers
max_of_three(X, Y, Z, Max) :-
    max(X, Y, TempMax),
    max(TempMax, Z, Max).

(ii) To find the average of odd and even elements from a list.

% Predicate to check if a number is even
even(X) :- 0 is X mod 2.

% Predicate to check if a number is odd
odd(X) :- 1 is X mod 2.

% Base case for summing even numbers
sum_evens([], 0, 0).
% Recursive case to sum even numbers
sum_evens([H|T], Sum, Count) :-
    even(H), !,
    sum_evens(T, TempSum, TempCount),
    Sum is TempSum + H,
    Count is TempCount + 1.
sum_evens([_|T], Sum, Count) :-
    sum_evens(T, Sum, Count).

% Base case for summing odd numbers
sum_odds([], 0, 0).
% Recursive case to sum odd numbers
sum_odds([H|T], Sum, Count) :-
    odd(H), !,
    sum_odds(T, TempSum, TempCount),
    Sum is TempSum + H,
    Count is TempCount + 1.
sum_odds([_|T], Sum, Count) :-
    sum_odds(T, Sum, Count).

% Predicate to calculate the average of numbers
average(Sum, Count, Avg) :-
    Count > 0,
    Avg is Sum / Count.

% Calculate averages of odd and even numbers in a list
average_odd_even(L, AvgOdd, AvgEven) :-
    sum_odds(L, SumOdds, CountOdds),
    average(SumOdds, CountOdds, AvgOdd),
    sum_evens(L, SumEvens, CountEvens),
    average(SumEvens, CountEvens, AvgEven).

OR

Q5

(a) Differentiate predicate and fact in Prolog programming. (3 marks)

Aspect	Predicate	Fact
Definition	A rule or relationship defined in the Prolog program.	A specific instance of a predicate known to be true.
Components	Consists of a predicate name and a number of arguments.	Comprises a predicate name and fixed arguments.
Purpose	Defines logical relationships between objects or states.	Represents ground truths or base cases.
Form	Can be defined using clauses, such as facts and rules.	Typically written without any conditions or logical implications.
Example	parent(X, Y) :- father(X, Y).	father(john, alice).

(b) Explain Hierarchical Planning. (4 marks)

Hierarchical Planning is a problem-solving approach used in artificial intelligence and automated planning systems. It involves breaking down a complex planning problem into a hierarchy of simpler subproblems, each of which can be solved independently or with minimal interaction. This hierarchical structure helps in managing the complexity of planning tasks and enables more efficient and modular planning.

Here's a detailed explanation of Hierarchical Planning:

1. Hierarchy Formation:
   • In Hierarchical Planning, the planning problem is decomposed into multiple levels of abstraction, forming a hierarchical structure.
   • The highest level represents the overall goal or objective to be achieved.
   • Subsequent levels represent increasingly detailed subgoals or subproblems.
2. Decomposition:
   • Each level of the hierarchy decomposes the problem into smaller, more manageable subproblems.
   • Decomposition can occur recursively until the subproblems are simple enough to be directly solved.
3. Abstraction:
   • Higher levels of the hierarchy deal with abstract goals and plans, while lower levels deal with more concrete details.
   • Abstraction helps in focusing on essential aspects of the problem at each level without getting bogged down in unnecessary details.
4. Integration:
   • Once solutions are found for the subproblems at lower levels, they are integrated to form solutions for higher-level subproblems.
   • This integration process ensures that the overall goal or objective is achieved by coordinating the solutions of the constituent subproblems.
5. Modularity:
   • Hierarchical Planning promotes modularity by encapsulating the complexity within each level of the hierarchy.
   • Each level can be independently designed, analyzed, and modified without affecting other levels, enhancing flexibility and scalability.
6. Efficiency:
   • By breaking down the problem into smaller subproblems, Hierarchical Planning can often lead to more efficient planning algorithms.
   • It allows for the reuse of common subplans across different instances of the problem, reducing redundant computation.
7. Example:
   • Consider a robot tasked with navigating through a complex environment to reach a target location.
   • The top-level goal could be to reach the destination safely.
   • Subsequent levels may involve planning paths to navigate around obstacles, avoiding collisions, and coordinating motion with perception and control subsystems.

(c) Write following Prolog programs: (7 marks)

(i) To check whether given string is palindrome or not.

% Base case: An empty string is a palindrome.
palindrome([]).

% Base case: A string with a single character is a palindrome.
palindrome([_]).

% Recursive rule: Check if the first and last characters are the same,
% then recursively check if the substring excluding the first and last
% characters is also a palindrome.
palindrome([X|Xs]) :-
    append(Middle, [X], Xs), % Split the list into middle and last character
    palindrome(Middle).      % Recursively check if the middle is a palindrome

% Predicate to check if a given string is a palindrome.
is_palindrome(String) :-
    string_chars(String, CharList), % Convert string to list of characters
    palindrome(CharList).           % Check if the list of characters is a palindrome

(ii) To find the length of a given list.

% Base case: The length of an empty list is zero.
length_list([], 0).

% Recursive rule: The length of a list is one more than the length of its tail.
length_list([_|T], Length) :-
    length_list(T, TailLength), % Recursively find the length of the tail
    Length is TailLength + 1.  % Increment the length by 1

% Predicate to find the length of a given list.
list_length(List, Length) :-
    length_list(List, Length). % Call the helper predicate to find the length